Sisyphus: A Cautionary Tale of Using Low-Degree Polynomial Activations in Privacy-Preserving Deep Learning
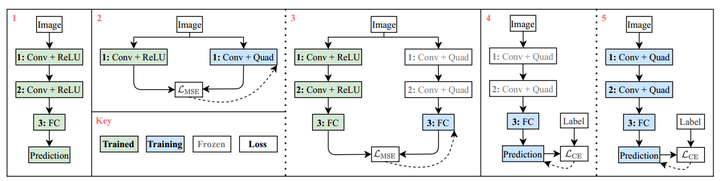 Steps for Quadratic Imitation Learning
Steps for Quadratic Imitation LearningAbstract
Privacy concerns in client-server machine learning have given rise to private inference (PI), where neural inference occurs directly on encrypted inputs. PI protects clients' personal data and the server’s intellectual property. A common practice in PI is to use garbled circuits to compute nonlinear functions privately, namely ReLUs. However, garbled circuits suffer from high storage, bandwidth, and latency costs. To mitigate these issues, PI-friendly polynomial activation functions have been employed to replace ReLU. In this work, we ask - Is it feasible to substitute all ReLUs with low-degree polynomial activation functions for building deep, privacy-friendly neural networks? We explore this question by analyzing the challenges of substituting ReLUs with polynomials, starting with simple drop-and-replace solutions to novel, more involved replace-and-retrain strategies. We examine the limitations of each method and provide commentary on the use of polynomial activation functions for PI. We find all evaluated solutions suffer from the escaping activation problem - forward activation values inevitably begin to expand at an exponential rate away from stable regions of the polynomials, which leads to exploding values (NaNs) or poor approximations.